Deductive vs. ampliative. Repletive vs. attenuative. Induction & abduction, starkly defined thereby.
Latest substantive edit: December 29, 2024 More edits to come.
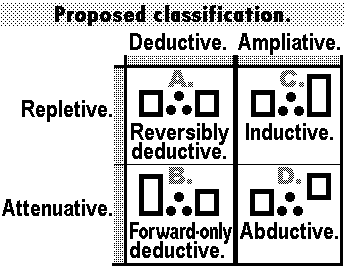
Uncluttered version of proposed square of
inference modes from Table 1 below.
To get going.
Deduction in logic is typically defined as inference in which the premises (when conjoined) entail the conclusion:—if the deduction’s premises are true, then its conclusion must be true. Many seem to regard induction in logic as the only non-deductive inference, or at least the only one feasible and worthwhile. Starting with C. S. Peirce, some have, instead, divided non-deductive inference,—properly known as ampliative inference,—into two modes: induction (≋ estimative generalization) and abduction (≋ surmise, explanatory guess);—and have not defined the two modes distinctly from each other in respect of entailment or its absence;—yet have argued, cogently, for the distinct modes’ reality.
Divide all inference into two modes,—(i) repletive and (ii) attenuative,—such that the premises are (i) entailed, or (ii) not entailed, BY the conclusion. Suppose that we re-define induction as repletive (and ampliative), and re-define abduction as attenuative (and ampliative). As an at least somewhat vindicative result, most of the inferences classed by Peirce as (i) inductive or (ii) abductive will remain so classed. However, inference 0f a hypothetical universal (e.g., a law of nature) from existential particulars, in a populous enough universe of discourse, becomes abductive rather than inductive. But even Peirce classed such inferences as abductive at least once, in 1903 (see Essential Peirce 2, p. 287, both 1st and 2nd paragraphs). “First, we guess it,” said physicist Richard Feynman to brief laughter during his “Finding New Laws” lecture of 1964-11-19.
Re-define induction and abduction? Peirce himself did not always adhere to traditional senses of words; for example he adopted the name “rhetoric” for methodology of science. Still, for made-up names instead of ones already in use, click the link for this post’s section on some made-up names for modes of inference.
Anyway, as a further nice result, definitive properties of four basic inference modes become consistently well distinguished from four desirable and variably achieved heuristic properties that have seldom if ever been recognized as a family, and one of which has been invoked by some to help define abduction. The four symmetrically patterned heuristic properties counterbalance,—one to one,—four limitations embedded,—one to one,—in four basic inference modes’ definitions. But the heuristic properties themselves have long seemed hard to quantify usefully or define precisely, to wit:
• an abductive conclusion’s simplicity in Peirce’s sense of naturalness of explanation—a semblance of feasibility or optimality;
• an inductive conclusion’s verisimilitude or likelihood (in Peirce’s sense), similarity to the premises—a semblance of probability;
• a forward-only deduction’s conclusion’s aspect of newness, dissimilarity, to the premises—a semblance of information or news; and
• a reversible deduction’s conclusion’s native complexity, its nontrivialness or depth—a semblance of data, givens, facts, factual relation instances.
Some more things related to the proposed definitions and classifications are summarized in Table 1 below.
| Inference modes. | Deduction = non-ampliative inference. Premises entail the conclusion or more. |
Ampliative inference = non-deductive inference (C.S. Peirce). Premises don’t entail the full conclusion. |
|---|---|---|
| Proposed name: Repletive inference = non-attenuative inference. Conclusion entails the premises or more. |
A.  Repletive-&-deductive: Reversible deduction (i.e., through equivalence). — Counterbalancingly, its conclusions gain worth by nontriviality, depth, complexity (from corollarial to theorematic). ⇝ Reversible deduction is the typical mode of inferences via PURE MATHS: structures of (1) space; (2) counting & measure; (3) group, ring, field; (4) order; |
C.  By proposed definition as By proposed definition as Repletive-&-ampliative: Induction from part to whole that entails the part. — Counterbalancingly, its conclusions gain worth by verisimilitude, likelihood (in Peirce’s sense: similarity of conclusion to premises). ⇝ Induction is the typical mode of inferences via STUDIES OF POSITIVE PHENOMENA IN GENERAL: (1) inverse optimization & allied descriptive; (2) statistics; (3) communication & control; (4) at least some of philosophy; |
| Proposed name: Attenuative inference = non-repletive inference. Conclusion doesn’t entail the full premises. |
B.  Attenuative-&-deductive: Forward-only deduction. — Counterbalancingly, its conclusions gain worth by newness of aspect, dissimilarity to premises. ⇝ Forward-only deduction is the typical mode of inferences via MATHS OF STRUCTURES OF ALTERNATIVES IN TIMELIKE PERSPECTIVES: (1) optima & feasible cases; (2) probabilities; (3) information; (4) facts (maths of logic); |
D.  By proposed definition as
By proposed definition as Attenuative-&-ampliative: Surmise, conjecture, abductive inference. — Counterbalancingly, its conclusions gain worth by plausibility à la Peirce: instinctual simplicity & naturalness. ⇝ Abductive inference is the typical mode of inferences via SCIENCES / STUDIES OF CONCRETE INDIVIDUAL PHENOMENA of: (1) motion; (2) matter; (3) life; (4) mind; |

- Table of contents.
- To get going. Table 1.
- Definitions of inference modes in terms of entailment and [etc.].
- Three notes.
- Trade-offs. Table 2. List. Table 3.
- Systematic opposition between definitive form and distinctive heuristics….
Table 4. Table 5. Table 6. - Let guesses seem guesses. Table 7.
- Rules, cases, facts.
- Inferring a rule from particulars: abductive vs. inductive.
- Abductive yet non-explanatory inference.
- “Reverse inferences”….
- Abductive inference and statistical syllogism.
- Fields that aim toward [various inference modes].
- Semantic discussion: “ampliative inference” ≡ “non-deductive inference”.
- Adjective choices.
- Made-up names. Table 8.
- Appendix: long quotes from C. S. Peirce’s 1898–91 Century Dictionary definitions of:
ampliation (3.);
ampliative;
inference;
induction (5.);
hypothesis (4.);
and, from Hibbert Journal, Peirce’s 1908 discussion of
simpler hypothesis.
Definitions of inference modes in terms of entailment and, just as well, truth/falsity-preservativeness.
Deductive and ampliative inferences DON’T and DO — respectively — ADD, as facts into their conclusions, things that have not been given as facts by their premises. But I couldn’t find reasonably simple names for inferences that DON’T and DO — respectively — OMIT, from their conclusions, things given as facts by their premises.
So, I picked out a couple of words — “repletive” and “attenuative” — that people may find handy. “Repletive” is pronounced re‑PLEE‑tiv. It rhymes with “depletive” and “completive”. I first discussed the words in a post “Inference terminology” to peirce-l 2015-04-07. (Under “Adjective choices” below, I discuss why the words seem better choices than others.) The premises of a repletive inference are entailed by, are deducible from, its conclusion. An attenuative inference is non-repletive.
Every inference is either deductive or ampliative (but not both) and is either repletive or attenuative (but not both), at least on assumptions of classical logic. Neither one of those two alternatives depends on the other.
The repletive-attenuative dichotomy, less prominent though it is, is worth a careful look, for it stands both analagous and crosswise to the deductive-ampliative dichotomy and adds some light in completing a regular four-way division (a tetrachotomy), one that frames both dichotomies. (Said tetrachotomy, displayed above as a square both in Table 1 and in Illustrative GIF 1, frames a third clarifying dichotomy, consisting of the two diagonals A.‑D. and B.‑C.)

Peirce
▼
Founder of the study
of abductive inference
Three notes.
1. Note on words. By standard definitions, all and only non‑deductive inference is ampliative inference, concluding in something extra in the sense of its not following purely from the premises. As said above, many call it “inductive” rather than “ampliative”. (Meanwhile, none of that pertains to mathematical induction, which is deductive.) In his classification of inferences, the logician, polymath, and composer of myriad dictionary definitions C. S. Peirce typically made, throughout most of his adult life (1860s–1914), a trichotomy of deduction, induction, and (under various labels) abduction, and called non‑deductive inference “ampliative”, which Peirce knew to be the adjective preferred over “synthetic” for non‑deductive judgment earlier by Sir W. Hamilton and before him by Kant’s translator Archbishop Thomson. See “Semantic discussion” far below. End of note.
2. Note on abductive inference. Abduction by my proposed (and seemingly original) definition is both ampliative and attenuative in both directions (between the premises as conjoined and the conclusion), ergo abductive in both directions, yet still tends to be retroductive, inferring a cause, reason, explanation, in only one direction. See more below under “Inferring a rule from particulars: abductive vs. inductive”. End of note.
3. Note on entailment etc. For simplicity’s sake, I refer to just the same thing for this discussion’s purposes, when I say things like “entailment properties” and when I say things like “truth-preservativeness and falsity-preservativeness”. End of note.
Trade-offs.
| Inference Mode & Elementary Forms. | Model-Theoretically. | Proof-Theoretically. | Informal Description. |
|---|---|---|---|
| Deductive, e.g.: p ∴ p. pq ∴ p. | Automatically preserves truth. | The premises entail the conclusion. | The conclusion does not go beyond the premises. |
| Ampliative, e.g.: p ∴ q. p ∴ pq. | Doesn’t automatically preserve truth. | The premises do not entail the conclusion. | The conclusion goes beyond the premises. |
| Repletive, e.g.: p ∴ p. p ∴ pq. | Automatically preserves falsity. | Falsity of the premise(s) (as conjoined) entails falsity of the conclusion. The premises are entailed by the conclusion. | The premises do not go beyond the conclusion. |
| Attenuative, e.g.: p ∴ q. pq ∴ p. | Doesn’t automatically preserve falsity. | Falsity of the premise(s) (as conjoined) does not entail falsity of the conclusion. The premises are not entailed by the conclusion. | The premises go beyond the conclusion. |
Each of the inference modes has its merits or virtues, as well as drawbacks or vices, in regard to the prospect of concluding in a truth or a falsehood:
- List: Security (futility) vs. opportunity (risk)
- Deductive inference does not decrease security / futility — i.e., does not increase opportunity / risk.
- Ampliative inference decreases security / futility — i.e., increases opportunity / risk — in some way.
- Repletive inference does not increase security / futility — i.e., does not decrease opportunity / risk.
- Attenuative inference increases security / futility — i.e., decreases opportunity / risk — in some way.
as prospects seen APART from their being counterbalanced in some sense by heuristic perspectives given by conclusions to premises.
I use the phrase “in some way” twice, in the bulleted list just above, in order to allude to the fact that an inference can be both ampliative and attenuative, i.e., it can at one same time increase risk (or whatever) in some way and decrease it in some other way. (Of course elementary inference, as a topic, does not exhaust the topic of security, opportunity, etc., and their increase and interplay in inquiry generally. Even at an elementary level, the prospects can be counterbalanced in some sense by heuristic perspectives given by conclusions to premises.)
Each merit or virtue comes with a flipside drawback or vice. Risk managers sometimes say, “opportunity equals risk,” and call them two sides of the same coin. In that spirit: security, safeness, equals futility — “nothing ventured, nothing gained.” Freud made much from the titanic fact that one tends to have less choice between pleasure and pain than between both and neither. Each of the above four inference modes works as a trade-off. On classical assumptions of two-valued logic, four mutually exclusive intersections of the above trade-offs, the above inference modes, necessarily arise and encompass all inferences:
| Inference modes | ⯆ ⯆ Deductive: NO INCREASE of opportunity / risk. |
⯆ ⯆ Ampliative ( = non-deductive): SOME INCREASE of opportunity / risk. |
|---|---|---|
|
Repletive: ⯈⯈
NO DECREASE of opportunity / risk. |
A. Reversible (i.e., equative) deduction. Repletive-&-deductive: NO decrease, NO increase, of opportunity / risk. |
C. Induction.
By proposed definition as: Repletive-&-ampliative: NO decrease, SOME increase, of opportunity / risk. |
|
Attenuative ⯈⯈
SOME DECREASE of opportunity / risk.( = non-repletive): |
B. Forward-only deduction. Attenuative-&-deductive: SOME decrease, NO increase, of opportunity / risk. |
D. Surmise, conjecture, abductive inference.
By proposed definition as: Attenuative-&-ampliative: SOME decrease, SOME increase, in different ways, of opportunity / risk. |
Any unilingual grab-bag of univocal propositions (or, more generally, terms, e.g., in calculations), no matter how one divides said bag’s contents into bag of conjoined premises and bag of conjoined conclusions, belongs to exactly two of the above four simple modes of inference, and to exactly one of their four intersections.
• Some deductive conclusions, despite true premises and conformity to standard definitions of deduction, will be just too obvious, blatantly redundant, which is worthwhile and needful in elementary rules of deduction but seldom elsewhere as far as I know. Conformity to the usual definitions of deduction, though needful in deduction, does not guarantee a deductive conclusion worthwhile in that it gives a non-obvious — new or nontrivial — aspect to the premises.
• Some ampliative conclusions, despite true premises and conformity to standard definitions of ampliative inference, will be arbitrary and capricious: all too unlikely or all too implausible.
Diverse special forms are usually developed in order to help in the practice of reaching worthwhile conclusions in correspondingly diverse major inference modes attended, as all of them are, by logically rooted risks and opportunities. Broad enough INVENTORY finds a common pattern of OPPOSITIONS between (A) definitive forms of major inference modes and (B) the modes’ distinctive heuristics. The definitive forms can occasion trade-offs whereby prospects for conclusions can be favorably re-balanced, so to speak, by the distinctive heuristics.
Systematic opposition between definitive form and distinctive heuristics of each of the main four mutually exclusive and collectively exhaustive modes of inference.

1959, M.C. Escher
Inferences may be worth classifying in the above four-fold manner because then four major inference modes will be defined in a uniform hard-core formal manner that exhausts the possibilities, by their basic internal entailment relations (or preservativeness or otherwise of truth and of falsity); meanwhile their various attempted heuristic merits —
◆ abductive conclusion’s plausibility (natural simplicity, in C. S. Peirce’s sense),
◆ inductive conclusion’s verisimilitude / likelihood (in Peirce’s sense: resemblance of conclusion to premises),
◆ forward-only-deductive conclusion’s new aspect, and
◆ reversibly-deductive conclusion’s nontriviality / depth
— can be treated as forming a systematic class of aspects of fruitfulness or promisingness of inference, with each of them related (as the compensatory opposite, in a sense) to its respective inference mode’s definitive internal entailment relations.
Those heuristic merits are difficult to quantify usefully or even to define exactly; yet, together with the entailment relations, they illuminingly form a regular system in which each heuristic merit helps to overcome, so to speak, the limitations of its inference mode’s definitive entailment relations. At any rate there is a fruitful tension between the heuristic merit and the entailment relations in each inference mode.
| Inferences | Deductive: | Ampliative: |
|---|---|---|
| Repletive: | A. Reversible deduction, e.g.: pq ∴ pq. Logically simple. Compensate with the nontrivial, complex, deep. |
C. Induction, e.g.: pq ∴ pqr. Adds new claim(s). Compensate with verisimilitude, likelihood (conclusion’s likeness to the old claims). |
| Attenuative: | B. Forward-only deduction, e.g.: pqr ∴ pq. Claims less, vaguer. Compensate with newness, by concision, of aspect. |
D. Abductive inference, e.g.: pq ∴ qr. Logically complicated. Compensate with natural simplicity (abductive plausibility). |
Notes about Table 4 above:
- Systematic oppositions hold along the diagonals.
- All the heuristic merits considered here are those of aspects that conclusions give to premises, not those of the actual inferring or reasoning itself, which reflects choices among more than one way up the mountain or molehill. Bennett 1988 introduced a quantitative concept for which he borrowed the phrase logical depth but, last I looked, some Gödelian incompleteness rule precludes a general way to prove that a given actual program’s running time is the shortest possible for reaching a given result. The Pythagorean theorem has very many proofs and is considered deep but not all its proofs are considered especially deep or very nontrivial, especially in the sense of “difficult” that is often enough (and understandably) allied to the idea of the nontrivial. Also see Cosma Shalizi on complexity measures (http link).
- (i) Natural simplicity and (ii) verisimilitude / likelihood contribute, in variable degree, to inclining the reasoner to believe or suspect a conclusion, at least until it is disconfirmed,
while, in systematic and symmetrical contrast to them,
(iii) novelty and (iv) nontriviality contribute, in variable degree, to inclining the reasoner to disbelieve or doubt a conclusion, at least until it becomes established.
Those things emerge along the deductive-ampliative axis, the strongest axis. The matter becomes more complex when one incorporates the risk-versus-doubt profile along the repletive-attenuative axis. This material needs work:
Table 5.Logically wrought decrease & increase of RISK versus
perspectivally courted increase & decrease of DOUBT.(A) Deductive conclusion
does not increase risk
YET can invite increase
of doubt.(B) Ampliative conclusion
increases risk
YET can invite sameness
or decrease of doubt.
(1) Repletive conclusion
does not decrease risk
YET can invite decrease
of doubt.
(2) Attenuative conclusion
decreases risk
YET can invite sameness
or increase of doubt.
(A1) Repletive-&-
deductive
conclusion can have
nontriviality, depth.
(A2) Attenuative-&-
deductive
conclusion can have
newness of aspect.
(B1) Inductive (defined as
repletive-&-ampliative)
conclusion can have
verisimilitude, likelihood.
(B2) Abductive (defined as
attenuative-&-ampliative)
conclusion can have
natural simplicity.
The result seems to be that, generally, in deduction, depth/nontrivialness and aspectual newness can invite doubt, but aspectual newness moreso; and that, generally, in ampliative inference, verisimilitude and natural simplicity can invite lessening of doubt, but verisimilitude moreso.
■■■■
■■■■
■■■■
■■■■
Now, an inference actually arising in a course of thought does not always present itself clearly. Hence, one may consider its seeming heuristic merit (such as plausibility), or its seeming purpose (such as explanation), in order to help one decide what mode of inference it ought to be framed as instancing.
It may even seem that one can pair the four entailment-related definitions one-to-one with four definitions in terms of heuristics and/or function. Yet, for example, deduction is not defined as explicative, making explicit the merely implicit, since an inference with the form “p∴p”, e.g., “all is well, ergo all is well”, is deductive but its conclusion extracts no new or nontrivial perspective from its premises. Furthermore and as already said, the heuristic merits themselves resist exact definition.
On the other hand, if no deduction were ever to make explicit the merely implicit, then no mind would bother with deductive reasoning. The heuristic merits deserve attention because, in the pervasive absence of all the heuristic merits, no mind would bother with any reasoning — explicit, consciously weighed inference — at all. Deduction, whether repletive or attenuative, would lose as much in general justification and rationale as induction and abductive inference would lose. Little in general would remain of inference, conscious or unconscious, mainly such activities as remembering, and free-associative supposing, which are degenerate inferences analogously as straight lines are degenerate conics.
| Inferences | Deductive: | Ampliative: |
|---|---|---|
| Repletive: | Reversible deduction, e.g.: … ∴ p, ∴ p, ∴ p, ∴ … . Fixated remembrance. |
Induction, e.g.: … ∴ p∨q, ∴ q, ∴ qr, ∴ … . Swelling expectation. |
| Attenuative: | Forward-only deduction, e.g.: … ∴ pq, ∴ q, ∴ q∨r, ∴ … . Dwindling notice. |
Abductive inference, e.g.: … ∴ p, ∴ q, ∴ r, ∴ … . Wild supposition. |

Source: ResearchGate
So, the proposed entailment-relational definitions of inductive and abductive inferences admit of pointless inferences. Yet this seeming problem may help solve a bigger problem. After all, the standard definitions of deduction admit of pointless inferences as well —vacuous deductions. Definitions of deduction would be just as slippery as those of induction and abductive inference if one were to try to define deduction generally in terms of purposive and heuristic properties rather than in terms of entailment relations (or, just as well, preservativeness and non-preservativeness of truth and falsity).
In the study of arguments, most of the theoretical interest will be in schemata and procedures that both (A) bring “blackboard validity” — conformity with the entailment-relational definition (and concomitant virtues) of the given inference mode — and also (B) ensure some modicum of the inference mode’s correlated mode of promise, such as natural simplicity (Peirce’s forms), a new aspect (the categorical syllogistic forms), etc. Together, such conformity and such promise relate inference modes to distinctive aims at explanation, prediction, etc.
Let guesses seem guesses.

Source: Academia.edu
Editor, director, now retired,
at the Peirce Edition Project.
But now that abduction is taken seriously, and so much attention has turned to its examination, we find that it is indeed a very slippery conception.
— Peirce scholar Nathan Houser in “The Scent of Truth” in Semiotica 153—1/4 (2005), 455–466.
An unslippery definition of abductive inference is reached naturally in the course of defining all the broadest inference modes in a hard-core way systematically via entailment relations (or, just as well, via truth/falsity-preservativeness), such that abductive inference is definable as both ampliative (not automatically preserving truth) and attenuative (not automatically preserving falsity) — the premises neither entail, nor are entailed by, the conclusion.

Yet, a guess — in the sense of a conjecture or surmise — is an inference insofar as it consists in acceptance of a proposition (or term), even if but tentatively, on the basis of some proposition(s) (or term(s)). Now, a guess ought to be at least somewhat a leap, out of a box so to speak, just as a deductive conclusion ought to be technically redundant, staying in a box. They are simply different trade-offs between opportunity (risk) and security (futility).
Ergo, let guessing seem guessing. Let the definition of abductive inference PLAINLY represent the potential wildness of abductive conclusions, ANALOGOUSLY as most definitions of deduction PLAINLY represent the technical redundancy and potential vacuity of deductive conclusions.
Let the potential wildness of abductive conclusions be seen as counterbalanced by the practice, discussed richly by Peirce and exemplifiable in various particular forms, of finding plausibility (natural simplicity), along with conceivably testable implications, analogously as the technical redundancy and potential vacuity of deductive conclusions are seen as counterbalanced by the practice, exemplifiable in various particular forms, of finding a new or nontrivial aspect, also conceivable further testability. Analogous remarks can be made about induction, verisimilitude / likelihood, and testability.

Source: Academia.edu
Thusly defined as both ampliative and attenuative, — and thusly distinguished as attenuative, from induction as repletive, — abductive inference would plainly have the autonomy found lacking by Tomis Kapitan (1949–2016) in “Peirce and the Autonomy of Abductive Reasoning” (PDF) in Erkenntnis 37 (1992), pages 1–26, an article discussed in Houser’s article linked above. (Kapitan also wrote “Abduction as Practical Inference”, published online in 2000 in the Digital Encyclopedia of Charles S. Peirce, reproduced at Commens.org.)
In other words, abductive inference would not boil down, in such analysis, to some application, practical or theoretical, of deduction and/or induction. Worthwhile, pertinent ideas about natural simplicity, explanatory power, pursuit-worthiness, etc., which contribute to the current slipperiness of definitions of abductive inference, would instead be further salient issues of abductive inference, neither explicitly contemplated in its definition nor axiomatized, postulated, or otherwise incorporated into the content of all abductive premises and conclusions. Such incorporation, besides the problems that Kapitan finds, would make one abductive conclusion into many conflicting ones, a continuum of potential conflicting ones, just by people’s differing soever fuzzily in the amounts of plausibility, economy, pursuit-worthiness, etc., that they assert in it. Define abductive inference by its form, not by its heuristics and functionality, just as with deduction, where the somewhat slippery but valuable and pertinent ideas of novelty, nontriviality, predictive power, etc., are further salient issues of deduction, neither explicitly contemplated in its standard definitions nor incorporated into the content of all deductions (and such couldn’t usefully be done deductively). Such spartanism at the elementary level need not and ought not go so far as to forbid explicitly qualifying the illative relation by saying “therefore, abductively,” or “therefore, deductively,” or the like, which very arguably Peirce would have endorsed.
Yet, some slipperiness remains, which the proposed definitions of the inference modes do not entirely remedy. I will take this up in the next subsection “inferring a rule from particulars”.
Rules, cases, facts.
Inferring a rule from particulars: abductive vs. inductive.
Given this post’s proposed definitions of induction and abduction (pace tradition), logically attenuative inference from one or more particulars to a rule is classed among abductive forms rather than inductive.
For example: “some fruit is sweet, ergo (rule) no fruit is not sweet (i.e., in logicians’ lingo, all fruit is sweet)”.
That fruit example concludes with a potentially very long shot from an existential particular to a (Boolean) hypothetical universal. The example does feel like a surmising, a conjecturing but, under the proposed definitions, we haven’t needed to guess its classification, since its classification is determined only by the overall relation of entailing and being entailed (or, just as well, truth/falsity preservativeness) between the premises as a whole and the conclusion as a whole.
Now, the original idea of induction was inference from particulars to a rule (see Peirce below); but one typically assumed the rule to be an (Aristotelian) existential universal, such that “All fruit is sweet” entails, deductively implies, its subaltern “Some fruit is sweet” (look up immediate inference). Even under the inference-mode definitions herein proposed, inference of an existential universal from particulars in a populous enough universe of discourse will, in some cases, be inductive, not abductive.
- In earlier years Peirce often portrayed abduction (calling it “hypothesis”) as inference from rule (all men are mortal) and fact (Socrates is mortal) to case (Socrates is a man), and as involving no generalization (see below for a quote from 1889–91). Later, Peirce at least once countenanced the abducing of rules from particulars. In his 1903 Syllabus of his Lowell lecture series Some Topics of Logic, he wrote (Essential Peirce 2, 287, in 1st paragraph, see at Commens):
The whole operation of reasoning begins with Abduction […]. Its occasion is a surprise. […]. The mind seeks to bring the facts, as modified by the new discovery, into order; that is, to form a general conception embracing them. In some cases, it does this by an act of generalization. In other cases, no new law is suggested, but only a peculiar state of facts that will “explain” the surprising phenomenon; and a law already known is recognized as applicable to the suggested hypothesis, so that the phenomenon, under that assumption, would not be surprising, but quite likely, or even would be a necessary result. […].
- One may wonder whether, in that passage, Peirce implicitly meant an INDUCTIVE generalization, not an abductive one, to a new law; but soon (in the 2nd paragraph on the same page 287 in EP 2, see at Google Books), Peirce wrote regarding deduction’s taking up an abduced hypothesis:
[…] either in the hypothesis itself, or in the pre-known truths brought to bear upon it, there must be a universal proposition, or Rule.
So, again, Peirce held at least in 1903 that a hypothesis abduced from particulars can contain a newly guessed rule.
Feynman asked, how do we find new laws? and emphasized that first, we guess them. Induction on the other hand, if defined as ampliative and repletive, seems oftenest concerned with estimating about one or another population or universe of discourse that requires not some universal quantification(s) “∀x ∀y Hxy” or the like that shoots its arrow through a hole in every axe at once, so to speak, but instead a collective predicate (such as the term “gamut”) attributing a distribution of properties, a relation, a percentage, etc., across that entire population or universe of discourse as one entire polyadic instance (at least implicitly), an ascription toward which an inductive inference seeks to expand the claims in its premises without squintingly narrowing its focus exclusively to rules up, up, and away, so to speak, from a variegated densely woven landscape.
Whew.
| Given a postulate or axiom of a universe of discourse of… |
There is a horse; ergo anything at all is a horse. ∃H ∴ ∀H. The above inference to a rule is: |
There is something both a horse & magnificent; ergo anything at all is, if a horse, then magnificent. ∃HM ∴ ∀(H→M). The above inference to a rule is: |
| …zero objects | Forward-only-deductive, but necessarily unsound. | Forward-only-deductive, but necessarily unsound. |
| …one object | Reversibly deductive. | Forward-only-deductive. |
| …zero or one object | Forward-only-deductive. | Forward-only-deductive. |
| …one or more objects | Inductive. | Abductive. |
| …zero or more objects | Abductive. | Abductive. |
To make the abductive equine example somewhat more realistic, suppose that the inference is something more like: There exists planet Earth with quite various countries crowded on it, among most of which are known to be distributed all known horses, and every such horse is known to be magnificent. Ergo, all horses are magnificent.

Source: BBC video via Cornell U. via YouTube.
[…]. In general, we look for a new law by the following process.
First, we guess it. Then we com- — w- – don’t laugh, that’s the - really true. Then we compute the consequences of the guess, to see what, if this is right, if this law that we guessed is right, we see what it would imply and then we compare those computation results to nature or we say compare to experiment or experience, — compare it directly with observations to see if it, if it works.
If it disagrees with experiment, — it’s wrong. In that simple statement is the key to science. It doesn’t make a difference how beautiful your guess is, it doesn’t matter how smart you are, who made the guess, or what his name is. If it disagrees with experiment, it’s wrong. That’s all there is to it. It’s therefore not unscientific to take a guess although many people who are not in science think it is. […].
— Richard Feynman, 11/19/1964, his Cornell U. Messenger Lecture series “The Character of Physical Law”, Lecture 7: “Seeking New Laws” (go to 16:29).
C. S. Peirce does at least once discuss a kind of abductive inference that concludes in a “generalization” to a new law (1903, see The Essential Peirce v. 2, p. 287, both paragraphs, see above). Peirce in earlier years described generalization as selective of the characters generalized (decreasing the comprehension while increasing the extension, see “Upon Logical Comprehension and Extension”, 1867, Collected Papers v. 2 ¶422, also in Writings v. 2, p. 84), and as casting out “sporadic” cases (“A Guess at the Riddle”, 1877–8 draft, see The Essential Peirce v. 1, p. 273). If, in the 1903 passage, he is discussing abductive inference by selective generalization quite generically, then any crude induction from the mass of experience seems to count as abductive instead.
Induction from sample to definite total population, as people actually frame it in practice, is sometimes not only ampliative but also attenuative — the conclusions do not always entail the premises, even though one usually thinks of induction as inferring from a part to a whole including the part.
There are ways to reframe the induction “half this [designated, indicated] actual sample is blue, so half the total is blue” so that its conclusion will entail its premise, ways that are perhaps to be favored over the example if they reflect better the inquirial interest involved in induction:
—one could say “some subset” or “some randomly drawn subset” (or the like) instead of “this actual sample” (or the like); or
—one could characterize this actual sample in the conclusion as well as in the premise (like a concluding graph that represents the actual measurements with a heavier line); or
—one could define a certain designated total population such that the definition is a kind of census explicitly designating each of the individuals in the population, and
—of course there are likely other ways that I haven’t thought of.
Such perspectives suit checking consistency by the deducibility of the premise from the conclusion and, applying probability calculations, deducing what would be the probability of drawing a given subset as a sample given alternate possible sets of parameters of the total population.
Abductive yet non-explanatory inference.
Take a famous example of abductive inference:
The lawn is wet this morning.
Whenever it rains at night, the lawn is wet the next morning.
Ergo [hypothetically] it rained last night.
Now, suppose that the example of abductive inference is instead:
It rained last night.
Whenever the lawn is wet in the morning, it has rained the previous night.
Ergo [hypothetically] the lawn is wet this morning.
That is not a usual abductive inference to a cause or reason, because it is hard to see how the hypothesized circumstance that the lawn is wet this morning would explain the fact that it rained last night.
Rather than try to see every individual effect in an individualized teleological light, it is simpler to note that abductive inference (in the sense of inference both ampliative and attenuative) can go in either direction between its set of premises and its set of conclusions, likewise as reversible deduction can. This view does not vitiate the connection between abductive inference and explanation, likewise as the analogous view about reversible deduction does not vitiate the connection between reversible deduction and proving a theorem or corollary.
Just as mathematical reversible deduction has a preferred direction given as its purpose of moving from things already postulated or proven (i.e., moving from reasons) to new conclusions, so likewise abductive inference in the sciences of concrete phenomena has a preferred direction by its purpose of moving from effects to causes (i.e., moving to reasons). Thus both abductive inference and reversible deduction can be both (A) defined in terms of entailment (or truth/falsity preservativeness) and (B) characterized by their respective purposes. It’s not a bad thing.
Mathematicians often enough move in the reverse direction in their “scratch work”, from thesis that needs proof, to something already postulated or proven — then, if every deductive step has been through an equivalence, they can simply reverse the order of the scratch work to produce the proof. Mobility in both directions seems less dazzling in abductive inference, at least insofar as abductive inferences (and non-mathematical inferences generally as Zadeh mentioned somewhere) tend to be less lengthy than reversible deductions which can become very long chains.
“Reverse inferences”: abduction vs. induction vs. deduction.
Abduction can seem deduction in reverse, e.g., using Peirce’s terms “rule”, “case”, and “fact”:
Deduction:
Rule: All food tastes good.
Case: This fish is food.
Ergo, deductively,
Fact: This fish tastes good.Abduction:
Fact [oddly]: This fish tastes good.
Rule: All food tastes good.
Ergo, abductively,
Case [plausibly]: this fish is food.
Yet the reversed Barbara deduction is not the abductive syllogism above. Instead, it is the capricious:
Fact: This fish tastes good.
Ergo: Case: This fish is food; and Rule: All food tastes good.
—which is both ampliative and repletive (i.e., inductive, not abductive, under present text’s proposal).
Also, the reversed traditional abductive syllogism is the capricious:
Case: This fish is food.
Ergo: Fact: This fish tastes good; and Rule: All food tastes good.
However, suppose that one makes not just a premise but a postulate (pr axiom) of the rule that all food tastes good. Then the rule will remain among the premises when the case and the fact switch places between the premise set and the conclusion. Under the postulate that all food tastes good:
• from the fact that this fish tastes good, one becomes able to induce the case that this fish is food; and
• from the case that this fish is food, one becomes able to (attenuatively) deduce the fact that this fish tastes good.
So, as a result of the proposed definitions of induction and abduction:
• an inference will be abductive if it extends an unpostulated rule to cover something as a case to explain a fact, and will not be the reverse of deduction of same fact from rule and case; and, by the same stroke,
• if the rule has been postulated, then the aforesaid inference will be inductive and its reverse will be deductive (& attenuative).
Abductive inference and statistical syllogism.
“It has rained every day for a week, ergo tomorrow it will rain.” Thusly framed, that inference is both ampliative and attenuative, hence abductive under the proposed definition. But it is just as natural to frame the thought as being, that it has rained every day for a week and that ergo tomorrow it will again rain, rain for the eighth consecutive day, etc., at which point the inference is framed as inductive; that seems much of its spirit. It turns into a kind of statistical syllogism, that is, a statistical induction concluding in a premise for an attenuative deduction — in this case, an induction from seven consecutive rainy days as of today to eight consecutive rainy days as of tomorrow, followed by an attenuative deduction (from the eight consecutive rainy days as of tomorrow) to a rainy day tomorrow, full stop. The restatement does justice to both the expansion, and the subsequent contraction, of focus of the original inference, by framing them separately in component inferences. When an inference, seemingly in a given mode, is so easily analyzed, reduced, into worthwhile component inferences in other modes, then it seems fairer to regard it as basically such a composition.
Fields that aim toward: reversible deduction; forward-only deduction; induction; and abductive inference.

Source: Herald-Tribune
The highest order of the imaginative intellect is always pre-eminently mathematical, or analytical; and the converse of this proposition is equally true.
— E. A. Poe, “American Poetry”, 1845, first paragraph, link to text.

Source:
Municipality of Aristotle
Reciprocation of premises and conclusion is more frequent in mathematics, because mathematics takes definitions, but never an accident, for its premises — a second characteristic distinguishing mathematical reasoning from dialectical disputations.
— Aristotle, Posterior Analytics, Bk. 1, Ch. 12, link to text.
Pure mathematics is marked by far-reaching networks of bridges of equivalences between sometimes the most disparate-seeming things. With good reason, popularizations often focus on examples of the metamorphosic power of mathematics. A topologist once told me that the statement “These two statements are equivalent” is itself one of the most common statements in mathematics. In a mundane example of a bridge by equivalence, in mathematical induction (actually a kind of deduction), one takes a thesis that is to be proved, and transforms it (in a fairly simple step) into the ancestral case and the heredity, conjoined. Once they’ve been separately proved (such is the hard part, also, I’ve read, often done by deductions through equivalences), then the mathematical induction itself, the induction step, consists in transforming (again, in a simple step) the conjunction of ancestral case with heredity back into the thesis, demonstrating the thesis. The reasoning in pure mathematics tends to be transformative, from one proposition (or compound) to another proposition equivalent to it and already proved or postulated or just easier or more promising to work with for the purpose at hand. When one’s scratch work proceeds through equivalences from a thesis to postulates or established theorems, then one can simply reverse the order of the scratch work for the proof of the thesis. Reverse mathematics, a project born in mathematical logic, takes up the question of just which mathematical theorems entail which sets of postulates as premises. This shows again the prominence of deduction through equivalences in pure mathematics. The reverse of the reasoning in pure mathematics is typically still reasoning by pure mathematics (even if with inquisitive guidance from mathematical logic).

Source: Columbia U
In an example contrasting to that, deduction of probabilities and statistical induction, two neighborly forms of quite different modes of inference, are seen as each other’s reverse or inverse, deduction of probabilities inferring (through forward-only deduction) from a total population’s parameters to particular cases, and statistical induction inferring in the opposite direction (e.g., in Jay L. Devore’s Probability and Statistics for Engineering and the Sciences, 8th Edition, 2011, beginning around “inverse manner” on page 5, into page 6). Such deductive fields as probability theory seem to involve the development of applications of pure mathematics in order to address “forward problems” in general, the problems of deducing solutions, predicting data, etc. from the given parameters of a universe of discourse, a total population, etc., with special attention to structures of alternatives and of implications. That description fits the deductive mathematics of optimization, probability (and uncertainty in Zadeh’s sense), and information (including algebra of information), and at least some of mathematical logic.
Now, statistical probability should not be nicknamed “inverse probability”, an obsolete phrase that comes from DeMorgan’s discussion of LaPlace and refers to a more specific idea, involving the method of Bayesian probability. On the other hand, the inverse of mathematics of optimization actually goes by such names as inverse optimization and inverse variations. On a third hand, inverse problem theory seems to concern inferring from observed effects to unobserved causes governed by known rules, and this seems a kind of abductive inference, albeit with a special emphasis on knowing the governing rules pretty comprehensively.
It is in the (comparatively) concrete sciences, the sciences of motion, matter, life, and mind, that abductive inference takes center stage. I’ll add some discussion here later.
Semantic discussion: “ampliative inference” ≡ “non-deductive inference”.
Question: does the phrase “ampliative inference” mean
• simply non-deductive inference (as I’ve taken it to mean) or, instead,
• inference that both (A) is non-deductive and (B) entails all its premises in its conclusion?
Peirce’s examples of abductive reasoning had premises that were not only far from entailing their conclusions, but also far (too far for a fair reframing to close the gap) from being entailed by their conclusions. He often classified abductive inference (which he also called hypothesis, retroduction, and presumption) as ampliative. Hence it is safe to say that his “ampliative” inference meant simply the non-deductive, not the both repletive and non-deductive. This was both (A) during the years that he treated abductive inference as based on sampling and as a rearrangement of the Barbara syllogism, and (B) afterwards, in the 1900s.
⯈ 1883:
We are thus led to divide all probable reasoning into deductive and ampliative, and further to divide ampliative reasoning into induction and hypothesis. [….]
—Page 143 in “A Theory of Probable Inference” in Studies in Logic. ⯇
⯈ 1889–91 Century Dictionary (“CD”), first edition: Peirce’s definition of “ampliative” (see below) says that it and “explicative” are alternates for the translative words “synthetic” and “analytic” in Kantian philosophy. Peirce also sets “explicative inference” and “ampliative inference” as “oppoosite” to each other in his bountiful definition of inference (see below) in CD. Note that explicative inference amounts to deduction of a not fully obvious conclusion; it doesn’t merely parrot one or more premises:
[….] Explicative inference, an inference which consists in the observation of new relations between the parts of a mental diagram (see above) constructed without addition to the facts contained in the premises. It infers no more than is strictly involved in the facts contained in the premises, which it thus unfolds or explicates. This is the opposite of ampliative inference, in which, in endeavoring to frame a representation, not merely of the facts contained in the premises, but also of the way in which they have come to present themselves, we are led to add to the facts directly observed. [….]
What may remain unclear to a reader of that passage is whether no ampliative conclusion omits a fact from its premises. Yet, if ampliative inference includes abductive inference (a.k.a. hypothesis), then an ampliative conclusion certainly can omit facts from the premises and remain ampliative, as one can see from Peirce’s many examples.
Meanwhile, the line between non-explicative and explicative deduction, i.e., between obvious and non-obvious deduction, seems not perfectly clear.
Also, the ampliative-deductive division is a dichotomy of all inferences. Explicative inferences, as forming a strict subset of deductions, are better opposed to an analogous strict subset of ampliative inferences, a subset consisting of ampliative inferences of which each conclusion accepts at least some definite matter from its premises, rather than veering arbitrarily into an unrelated matter. Non‑explicative deductions parrot too much, as opposed to capricious ampliative inferences that parrot too little.
• Kant’s analytic judgments = explicative conclusions = some deductive conclusions, but not the blatantly redundant ones, rather those that give a new or nontrivial aspect to their premises.
• Kant’s synthetic judgments = ampliative conclusions, from mild to wild, from likely or plausible to unlikely and implausible.
Anyway, like most who contemplate inference modes, Peirce usually refers to deductive (rather than explicative) inference in discussing inference in mathematics, traditional categorical syllogisms, and mathematical probabilities. ⯇
⯈ 1892: Peirce treats “non-deductive” and “ampliative” as alternate labels for the same kinds of inference, as follows in “The Doctrine of Necessity Examined”, § II, 2nd paragraph:
[….] Non-deductive or ampliative inference is of three kinds: induction, hypothesis, and analogy. If there be any other modes, they must be extremely unusual and highly complicated, and may be assumed with little doubt to be of the same nature as those enumerated. For induction, hypothesis, and analogy, as far as their ampliative character goes, that is, so far as they conclude something not implied in the premises, depend upon one principle and involve the same procedure. All are essentially inferences from sampling. [….]
(Throughout the years, he usually regarded analogy as a combination of induction and hypothetical inference.) ⯇
⯈ 1900s: Peirce ceased holding that hypothetical (a.k.a. abductive, a.k.a. retroductive) inference aims at a likely conclusion from parts considered as samples, and argued instead that abductive inference aims at a plausible, natural, instinctually simple explanation as (provisional) conclusion and that it introduces an idea new to the given case, while induction merely extends to a larger whole of cases an idea already asserted (not merely framed) in the premises. This does not mean that only abductive inference is ampliative; instead at most it means that only abductive inference is ampliative with regard to ideas, while induction is ampliative of the extension of ideas. (I’m unsure whether Peirce regarded abduced ideas as being definable by comprehension a.k.a. intension (as opposed to extension a.k.a. denotation). ⯇
⯈ 1902: In a draft, regarding his past treatment of abductive inference, Peirce wrote,
I was too much taken up in considering syllogistic forms and the doctrine of logical extension and comprehension, both of which I made more fundamental than they really are.
— Collected Papers v. 2, ¶ 102. ⯇
Adjective choices.
“Repletive” (re-PLEE-tiv) seems a better adjective than “retentive” for non-attenuative inference (although maybe it’s just me), because “retentive” suggests not just keeping the premises, but restraining them or the conclusions in one sense or another. The word “preservative”, to convey the idea of preserving the premises into the conclusions, would lead to confusion with the more usual use of “preservative” in logic’s context to pertain to truth-preservativeness (not to mention falsity-preservativeness). If people dislike the word “repletive” for the present purpose, then I suppose that “transervative” would do.
“Attenuative” (a-TEN-yoo-ay-tiv) seems much better than “precisive” or “reductive” for non-repletive inference. The adjective “precisive” seems applicable only abstrusely to an apparently dis-precisive inference in the form of “p, ergo p or q”. Attenuative inference generally narrows logical focus, but in doing this it renders vague (i.e., omits) some of that which had been in focus. “Reductive” may be less bad than “precisive” in those respects but is rendered too slippery by irrelevant senses clinging from other contexts and debates.
Made-up names.
| Inferences | Deduction: | Ampliative inference: |
|---|---|---|
| Repletive inference: |
A. Equiduction (ē-kwi-duk′ -sho̤n) ≡ reversible deduction. Conclusion tries to be basatile (bā′- sa̤-tīl) (i.e., nontrivial, deep, complex). |
C. Pluduction (plo̅o̅-duk′ -sho̤n) ≋ induction. Conclusion tries to be veteratile (ve′ -te̤-ra̤-tīl) (i.e., verisimilar, likely, in Peirce’s sense). |
| Attenuative inference: |
B. Minuduction (mī-nū-duk′ -sho̤n) ≡ forward-only deduction. Conclusion tries to be novatile (nō′ -va̤-tīl) (i.e., new in aspect). |
D. Mercuduction (mėr-kū-duk′ -sho̤n) ≋ abductive inference. Conclusion tries to be aviatile (ā′ -vi-a̤-tīl) (i.e., plausible à la Peirce: instinctually simple-&-natural, facile. • Maybe “alduction” would be better than “mercuduction” |
APPENDIX: C. S. Peirce’s definitions of ampliation 3. (in logic), ampliative, inference, induction 5. (in logic), and hypothesis 4., in 1889–91 in the Century Dictionary; and his discussion of simpler hypothesis in 1908 in Hibbert Journal.
Here are two excerpts from 1889–91 (and identically in 1911) from the Century Dictionary’s definitions of “ampliation” and “ampliative”, of which Peirce was in charge of the definitions, per the list of words compiled by the Peirce Edition Project’s former branch at the Université de Québec à Montréal (UQÁM).
ampliation (am-pli-ā′ sho̤n) […] — 3. In logic, such a modification of the verb of a proposition as makes the subject denote objects which without such modification it would not denote, especially things existing in the past and future. Thus, in the proposition, “Some man may be Antichrist,” the modal auxiliary may enlarges the breadth of man, and makes it apply to future men as well as to those who now exist.
ampliative (am′ pli-ạ̄-tiv) […] Enlarging; increasing; synthetic. Applied — (a) In logic, to a modal expression causing an ampliation (see ampliation, 3); thus, the word may in “Some man may be Antichrist” is an ampliative term. (b) In the Kantian philosophy, to a judgment whose predicate is not contained in the definition of the subject: more commonly termed by Kant a synthetic judgment. [“Ampliative judgment” in this sense is Archbishop Thomson’s translation of Kant’s word Erweiterungsurtheil, translated by Prof. Max Müller “expanding judgment.”]
No subject, perhaps, in modern speculation has excited an intenser interest or more vehement controversy than Kant’s famous distinction of analytic and synthetic judgments, or, as I think they might with far less of ambiguity be denominated, explicative and ampliative judgments. Sir W. Hamilton.
— Century Dictionary, p. 187, in Part 1: A – Appet., 1889–91, of Volume 1 of 6, first edition, and identically on p. 187 in Volume 1 of 12, 1911 edition. The brackets around the sentence mentioning Archbishop Thomson are in the originals.
Peirce for his own part focused on the deductiveness or ampliativeness of inference, not of ready-made judgments (he once said that a Kantian synthetic judgment is a “genuinely dyadic” judgment, see Collected Papers v. 1 ¶ 475). Peirce argued that mathematics aims at theorematic deductions that require experimentation with diagrams, a.k.a. schemata, and that it concerns purely hypothetical objects. (So much for Kant’s synthetic a priori.)
The following is from the first edition, 1889–91, CD volume 3, CD part 11 Ihleite – Juno, CD pages 3080–1. Peirce was in charge of the CD’s definition of inference, per the list of words compiled by the Peirce Edition Project’s former branch at the Université de Québec à Montréal (UQÁM). I recently typed the text out from the Internet Archive, so I’d suggest checking it against the Internet Archive version if you quote or copy from the resultant text below. Let me know if you find an error.
inference (in′ fėr-ens), n. [= F. inférence = Sp. Pg. inferencia, ˂ ML. inferentia, inference, ˂ L. inferre, infer: see infer.] 1. The formation of a belief or opinion, not as directly observed, but as constrained by observations made of other matters or by beliefs already adopted; the system of propositions or judgments connected together by such an act in a syllogism — namely, the premises, or the judgment or judgments which act as causes, and the conclusion, or the judgment which results as an effect; also, the belief so produced. The act of inference consists psychologically in constructing in the imagination a sort of diagram or skeleton image of the essentials of the state of things represented in the premises, in which, by mental manipulation and contemplation, relations that had not been noticed in constructing it are discovered. In this respect inference is analogous to experiment, where, in place of a diagram, a simplified state of things is used, and where the manipulation is real instead of mental. Unconscious inference is the determination of a cognition by previous cognitions without consciousness or voluntary control. The lowest kind of conscious inference is where a proposition is recognized as inferred, but without distinct apprehension of the premises from which is has been inferred. The next lowest is the simple consequence, where a belief is recognized as caused by another belief, according to some rule or psychical force, but where the nature of this rule or leading principle is not recognized, and it is in truth some observed fact embodied in a habit of inference. Such, for example, is the celebrated inference of Descartes, Cogito, ergo sum (‘I think, therefore I exist’). Higher forms of inference are the direct syllogism (see syllogism); apagogic inference, or the reductio ad absurdum, which involves the principle of contradiction; dilemmatic inference, which involves the principle of exluded middle; simple inferences turning upon relations; inferences of transposed quantity (see below); and the Fermatian inference (see Fermatian). Scientific inferences are either inductive or hypothetic. See induction, 5, and analogy, 3.
2. Reasoning from effect to cause; reasoning from signs; conjecture from premises or criteria; hypothesis.
An excellent discourse on . . . the inexpressible happiness and satisfaction of a holy life, with pertinent inferences to prepare us for death and a future state.
Evelyn, Diary, Nov. 21, 1703.He has made not only illogical inferences, but false statements.
Macaulay, Mitford’s Hist. Greece.Take, by contrast, the word inference, which I have been using: it may stand for the act of inferring, as I have used it; or for the connecting principle, or inferentia, between premises and conclusions; or for the conclusion itself.
J. H. Newman, Gram. of Assent, p. 254.Alternative inference. See alternative. — Ampliative inference. See explicative inference, below. — Analogical inference, the inference that a certain thing, which is known to possess a certain number of characters belonging to a limited number of objects or to one only, also possesses another character common to those objects. Such would be the inference that Mars is inhabited, owing to its general resemblance to the earth. Mill calls this inference from particulars to particulars, and makes it the basis of induction. — Apagogical inference, an inference reposing on the principle of contradiction, that A and not-A cannot be predicated of the same subject; the inference that a proposition is false because it leads to a false conclusion. Such is the example concerning mercury, under deductive inference, below. — Comparative inference. See comparative. — Complete inference, an inference whose leading principle involves no matter of fact over and above what is implied in the conception of reasoning or inference: opposed to incomplete inference, or enthymeme. Thus, if a little girl says to hereself, “It is naughty to do what mamma tells me not to do; but mamma tells me not to squint; therefore it is naughty to squint,” this is a complete inference; while if the first premise does not completely and explicitly appear in her thought, although really operative in leading her to the conclusion, it ceases to be properly a premise, and the inference is incomplete. — Correct inference, an inference which conforms to the rules of logic, whether the premises are true or not. — Deductive inference, inference from a general principle, or the application of a precept or maxim to a particular case recognized as coming under it: a phrase loosely applied to all explicative inference. Example: Mercury is a metal, and mercury is a liquid; hence, not all metals are solid. The general rule here is that all metals are solid, which is concluded to be false, because the necessary consequence that mercury would be solid is false. — Direct deductive inference, the simple inference from an antecedent to a consequent, in virtue of a belief in their connection as such. Example: All men die; Enoch and Elijah were men; therefore they must have died. — Disjunctive inference. Same as alternative inference. — Explicative inference, an inference which consists in the observation of new relations between the parts of a mental diagram (see above) constructed without addition to the facts contained in the premises. It infers no more than is strictly involved in the facts contained in the premises, which it thus unfolds or explicates. This is the opposite of ampliative inference, in which, in endeavoring to frame a representation, not merely of the facts contained in the premises, but also of the way in which they have come to present themselves, we are led to add to the facts directly observed. Thus, if I see the full moon partly risen above the horizon, it is absolutely out of my power not to imagine the entire disk as completed, and then partially hidden; and it will be an addition to and correction of this idea if I then stop to reflect that since the moon rose last the hidden part may have been torn away; the inference that the disk of the moon is complete is an irresistible ampliative inference. All the demonstrations of mathematics proceed by explicative inferences. — Fermatian inference. See Fermatian. — Hypothetic inference, the inference that a hypothesis, or supposition, is true because its consequences, so far as tried, have been found to be true; in a wider sense, the inference that a hypothesis resembles the truth as much as its consequences have been found to resemble the truth. Thus, Schliemann supposes the story of Troy to be historically true in some measure, on account of the agreement of Homer’s narrative with the findings in his excavations, all of which would be natural results of the truth of the hypothesis. — Immediate inference. See immediate. — Incomplete inference. See complete inference, above. — Indirect inference, any inference reposing on the principle that the consequence of a consequence is itself a consequence. The same inference will be regarded as direct or indirect, according to the degree of importance attached to the part this principle plays in it. Example: All men die; but if Enoch and Elijah died, the Bible errs; hence, if Enoch and Elijah were men, the Bible errs. — Inductive inference. See induction, 5. — Inference of transposed quantity, any inference which reposes on the fact that a certain lot of things is infinite in number, so that the inference would lose its cogency were this not the case. The following is an example: Every Hottentot kills a Hottentot; but nobody is killed by more than one person; consequently, every Hottentot is killed by a Hottentot. If the foolish first premise is supposed to hold good of the finite number of Hottentots who are living at any one time, the inference is conclusive. But if the infinite succession of generations is taken into account, then each Hottentot might kill a Hottentot of the succeeding generation, say one of his sons, yet many might escape being killed.Tetrast Note 1: Peirce previously discussed inference of transposed quantity in 1881: Google on "Peirce" "every Texan kills". End of note. — Leading principle of inference, the formula of the mental habit governing an inference. — Necessary inference, an explicative inference in which it is logically impossible for the premises to be true without the truth of the conclusion.Tetrast Note 2: Peirce had necessary inference and probable inference together forming a dichotomy of all inferences except non-explicative deductions. Probable inference included:
—deduction of a mathematically probable conclusion,
—induction, &
—abduction.
But, by the 1900s, he regarded abduction as seeking to be plausible rather than probable in the inductive sense. By that standard, deductions of optimal and feasible solutions should also be classed as plausible inferences. Mathematics of optimization (longer known as linear and nonlinear programming) was not yet a discipline while Peirce lived. Also in later years he ascribed verisimilitude (which he also called likelihood) to worthwhile inductions. On such distinctions in general, see my Plausibility, verisimilitude, novelty, nontriviality, versus optima, probabilities, information, givens.. End of note. — Probable inference, a kind of inference embracing all ampliative and some explicative inference, in which the premises are recognized as possibly true without the truth of the conclusion, but in which it is felt that the reasoner is following a rule which may be trusted to lead him to the truth in the main and in the long run. — Ricardian inference, the mode of inference employed by Ricardo to establish his theory of rent. See Ricardian. — Statistical inference, an inference in regard to the magnitude of a quantity, where it is concluded that a certain value is the most probable, and that other possible values gradually fall off in probability as they depart from the most probable value. All of the inferences of those sciences which are dominated by mathematics are of this character. = Syn. Analysis, Anticipation, Argument, Argumentation, Assay, Assent, Assumption, Conclusion, Conjecture, Conviction, Corollary, Criterion, Decision, Deduction, Demonstration, Dilemma, Discovery, Elench, Enthymeme, Examination, Experiment, Experimentation, Finding, Forecast, Generalization, Guess, Hypothesis, Illation, Induction, Inquiry, Investigation, Judgment, Lemma, Moral, Persuasion, Porism, Prediction, Prevision, Presumption, Probation, Prognostication, Proof, Ratiocination, Reasoning, Research, Sifting, Surmise, Test, Theorem, Verdict. Of these words, illation is a strict synonym for inference in the first and principal meaning of the latter word, but is pedantic and little used. Reasoning has the same meaning but is not used as a relative noun with of; thus, we speak of the inference of the conclusion from the premises, and of reasoning from the premises to the conclusion. A reasoning may consist of a series of acts of inferences. Ratiocination is abstract and severe reasoning, involving only necessary inferences. Conclusion differs from inference mainly in being applied preferentially to the result of the act called inference; but conclusion would further usually imply a stronger degree of persuasion than inference. Conviction and persuasion denote the belief attained, or its attainment, from a psychological point of view, while inference, illation, reasoning, ratiocination, and conclusion direct attention to the logic of the procedure. Conviction is perhaps a stronger word than persuasion, and more confined to serious and moral inferences. Discovery is the inferential or other attainment of a new truth. Analysis, assay, examination, experiment, experimentation, inquiry, investigation, and research are processes analogous to inference, and also involving acts of inference. Anticipation, assent, assumption, and presumption express the attainment of belief either without inference or considered independently of any inference. Presumption is used for a probable inference or for the ground of it. Argument, argumentation, demonstration, and proof set forth the logic of inferences already drawn. Criterion and test are rules of inference. Elench is that relation between the premises which compels assent to the conclusion; it is translated “evidence” in Heb. xi. 1, where an intellectual conclusion is meant. Corollary, deduction, dilemma, enthymeme, forecast, generalization, induction, lemma, moral, porism, prediction, prevision, prognostication, sifting, and theorem are special kinds of inference. (See those words). Conjecture, guess, hypothesis, and surmise are synonyms of inference in its secondary sense. Guess and surmise are weaker words.
The following is “induction, 5.” in the first edition, 1889–91, CD volume 3, CD part 11 Ihleite – Juno, CD page 3068. Peirce was in charge of the CD’s definition of induction, per the list of words compiled by the Peirce Edition Project’s former branch at the Université de Québec à Montréal (UQÁM).
induction […] 5. In logic, the process of drawing a general conclusion from particular cases; the inference from the character of a sample to that of the whole lot sampled. Aristotle’s example is: Man, the horse, and the mule are animals lacking a gall-bladder; now, man, the horse, and the mule are long-lived animals; hence, all animals that lack the gall-bladder are long-lived. Logicians usually make it essential to induction that it should be an inference from the possession of a character by all the individuals of the sample to its possession by the whole class; but the meaning is to be extended so as to cover the case in which, from the fact that a character is found in a certain proportion of individuals of the sample, its possession by a like proportion of individuals of the whole lot sampled is inferred. Thus, if one draws a handful of coffee from a bag, and, finding every bean of the handful to be a fine one, concludes that all the beans in the bag are fine, he makes an induction; but the character of the inference is essentially the same if, instead of finding that all the beans are fine, he finds that two thirds of them are fine and one third inferior, and thence concludes that about two thirds of all the beans in the bag are fine. On the other hand, induction, in the strict sense of the word, is to be distinguished from such methods of scientific reasoning as, first, reasoning by signs, as, for example, the inference that because a certain lot of coffee has certain characters known to belong to coffee grown in Arabia, therefore this lot grew in Arabia; and, second, reasoning by analogy, where, from the possession of certain characters by a certain small number of objects, it is inferred that the same characters belong to another object, which considerably resembles those objects named, as the inference that Mars is inhabited because the earth is inhabited. But the term induction has a second and wider sense, derived from the use of the term inductive philosophy by Bacon. In this second sense, namely, every kind of reasoning which is neither necessary nor a probable deduction, and which, though it may fail in a given case, is sure to correct itself in the long run, is called an induction. Such inference is more properly called ampliative inference. Its character is that, though the special conclusion drawn might not be verified in the long run, yet similar conclusions would be, and in the long run the premises would be so corrected as to change the conclusion and make it correct. Thus, if, from the fact that female births are generally in excess among negroes, it is inferred that they will be so in the United States during any single year, a probable deduction is drawn, which, even if it happens to fail in the special case, will generally be found true. But if, from the fact that female births are shown to be in excess among negroes in any one census of the United States, it is inferred that they are generally so, an induction is made, and if it happens to be false, then on continuing that sort of investigation, new premises will be obtained from other censuses, and thus a correct general conclusion will in the long run be reached. Induction, as above defined, is called philosophical or real induction, in contradistinction to formal or logical induction, which rests on a complete enumeration of cases and is thus induction only in form. A real induction is never made with absolute confidence, but the belief in the conclusion is always qualified and shaded down. Socratic induction is the formation of a definition from the consideration of single instances. Mathematical induction, so called, is a peculiar kind of demonstration introduced by Fermat, and better termed Fermatian inference. This demonstration, which is indispensable in the theory of numbers, consists in showing that a certain property, if possessed by any number whatever, is necessarily possessed by the number next greater than that number, and then in showing that the property in question is in fact possessed by some number, N; whence it follows that the property is possessed by every number greater than N.
Socrates used a kind of induccion by asking many questions, the whiche when thei were graunted he broughte thereupon his confirmacion concerning the present controversie; which kinde of argument hath his name of Socrates himself, called by the learned Socratic induction.
Sir T. Wilson, Rule of Reason.Our memory, register of sense,
And mould of arts, as mother of induction.
Lord Brooke, Human Learning (1633), st. 14.Inductions will be more sure, the larger the experience from which they are drawn.
Bancroft, Hist. Const. I. 5.
The following is “hypothesis, 4.” in the first edition, 1889–91, CD volume 3, CD part 10 Halve – Iguvine, CD page 2959. Peirce was in charge of the CD’s definition of hypothesis, per the list of words compiled by the Peirce Edition Project’s former branch at the Université de Québec à Montréal (UQÁM).
hypothesis […]. 4. The conclusion of an argument from consequent and antecedent; a proposition held to be probably true because its consequences, according to known general principles, are found to be true; the supposition that an object has a certain character, from which it would necessarily follow that it must possess other characters which it is observed to possess. The word has always been applied in this sense to theories of the planetary system. Kepler held the hypothesis that Mars moves in an elliptical orbit with the sun in one focus, describing equal areas in equal times, the ellipse having a certain size, shape, and situation, and the perihelion being reached at a certain epoch. Of the three coordinates of the planet’s position, two, determining its apparent position, were directly observed, but the third, its varying distance from the earth, was the subject of hypothesis. The hypothesis of Kepler was adopted because it made the apparent places just what they were observed to be. A hypothesis is of the general nature of an inductive conclusion, but it differs from an induction proper in that it involves no generalization, and in that it affords an explanation of observed facts according to known general principles. The distinction between induction and hypothesis is illustrated by the process of deciphering a despatch written in a secret alphabet. A statistical investigation will show that in English writing, in general, the letter e occurs far more frequently than any other; this general proposition is an induction from the particular cases examined. If now the despatch to be deciphered is found to contain 26 characters or less, one of which occurs much more frequently than any of the others, the probable explanation is that each character stands for a letter, and the most frequent one for e: this is hypothesis. At the outset, this is a hypothesis not only in the present sense, but also in that of being a provisional theory insufficiently supported. As the process of deciphering proceeds, however, the inferences become more and more probable, until practical certainty is attained. Still the nature of the evidence remains the same; the conclusion is held true for the sake of the explanation it affords of observed facts. Generally speaking, the conclusions of hypothetic inference cannot be arrived at inductively, because their truth is not susceptible of direct observation in single cases; nor can the conclusions of inductions, on account of their generality, be reached by hypothetic inference. For instance, any historical fact, as that Napoleon Bonapart once lived, is a hypothesis; for we believe the proposition because its effects — current tradition, the histories, the monuments, etc. — are observed. No mere generalization of observed facts could ever teach us that Napoleon lived. Again, we inductively infer that every particle of matter gravitates toward every other. Hypothesis might lead to this result for any given pair of particles, but could never show that the law is universal. The chief precautions to be used in adopting hypotheses are two: first, we should take pains not to confine our verifications to certain orders of effects to which the supposed fact would give rise, but to examine effects of every kind; secondly, before a hypothesis can be regarded as anything more than a suggestion, it must have produced successful predictions. For example, hypotheses concerning the luminiferous ether have had the defect that they would necessitate certain longitudinal oscillations to which nothing in the phenomenon corresponds; and consequently these theories ought not to be held as probably true, but only as analogues of the truth. As long as the kinetical theory of gases merely explained the laws of Boyle and Charles, which it was constructed to explain, it had little importance; but when it was shown that diffusion, viscosity, and conductibility in gases were connected and subject to those laws which theory had predicted, the probability of the hypothesis became very great.
I asked him what he thought of Locusts, and whether the History might not be better accounted for, supposing them to be the winged Creatures that fell so thick about the Camp of Israel? but by his answer it appear’d that he had never heard of any such Hypothesis.
Maundrell, Aleppo to Jerusalem, p. 61.We have explained the phænomena of the heavens and of our sea by the power of gravity. . . . . But hitherto I have not been able to discover the cause of those properties of gravity from phænomena, and I frame no hypothesis; for whatever is not deduced from the phænomena is to be called an hypothesis; and hypotheses, whether metaphysical or physical, whether occult qualities or mechanical, have no place in experimental philosophy.
Newton, Principia (tr. by Motte), iii.
The following is from Peirce’s 1908 discussion of the idea of simpler hypothesis, from near the end of IV in “A Neglected Argument for the Reality of God” (via Wikisource with added good notes), originally published (incompletely) in Hibbert Journal v. 7 and less incompletely in Collected Papers v. 6 and Essential Peirce v. 2. For the whole essay go to https://gnusystems.ca/CSPgod.htm#na0. By “il lume naturale” is understood “the natural light of reason”.
Modern science has been builded after the model of Galileo, who founded it on il lume naturale. That truly inspired prophet had said that, of two hypotheses, the simpler is to be preferred; but I was formerly one of those who, in our dull self-conceit fancying ourselves more sly than he, twisted the maxim to mean the logically simpler, the one that adds the least to what has been observed, in spite of three obvious objections: first, that so there was no support for any hypothesis; secondly, that by the same token we ought to content ourselves with simply formulating the special observations actually made; and thirdly, that every advance of science that further opens the truth to our view discloses a world of unexpected complications. It was not until long experience forced me to realise that subsequent discoveries were every time showing I had been wrong,— while those who understood the maxim as Galileo had done, early unlocked the secret,— that the scales fell from my eyes and my mind awoke to the broad and flaming daylight that it is the simpler Hypothesis in the sense of the more facile and natural, the one that instinct suggests, that must be preferred; for the reason that unless man have a natural bent in accordance with nature’s, he has no chance of understanding nature at all. Many tests of this principal and positive fact, relating as well to my own studies as to the researches of others, have confirmed me in this opinion; and when I shall come to set them forth in a book, their array will convince everybody. Oh no! I am forgetting that armour, impenetrable by accurate thought, in which the rank and file of minds are clad! They may, for example, get the notion that my proposition involves a denial of the rigidity of the laws of association: it would be quite on a par with much that is current. I do not mean that logical simplicity is a consideration of no value at all, but only that its value is badly secondary to that of simplicity in the other sense.
. . . . |



